Chapitre 12: Théorème de Thalès.
Agrandissement/
Réduction.
Homothétie.

1.Thalès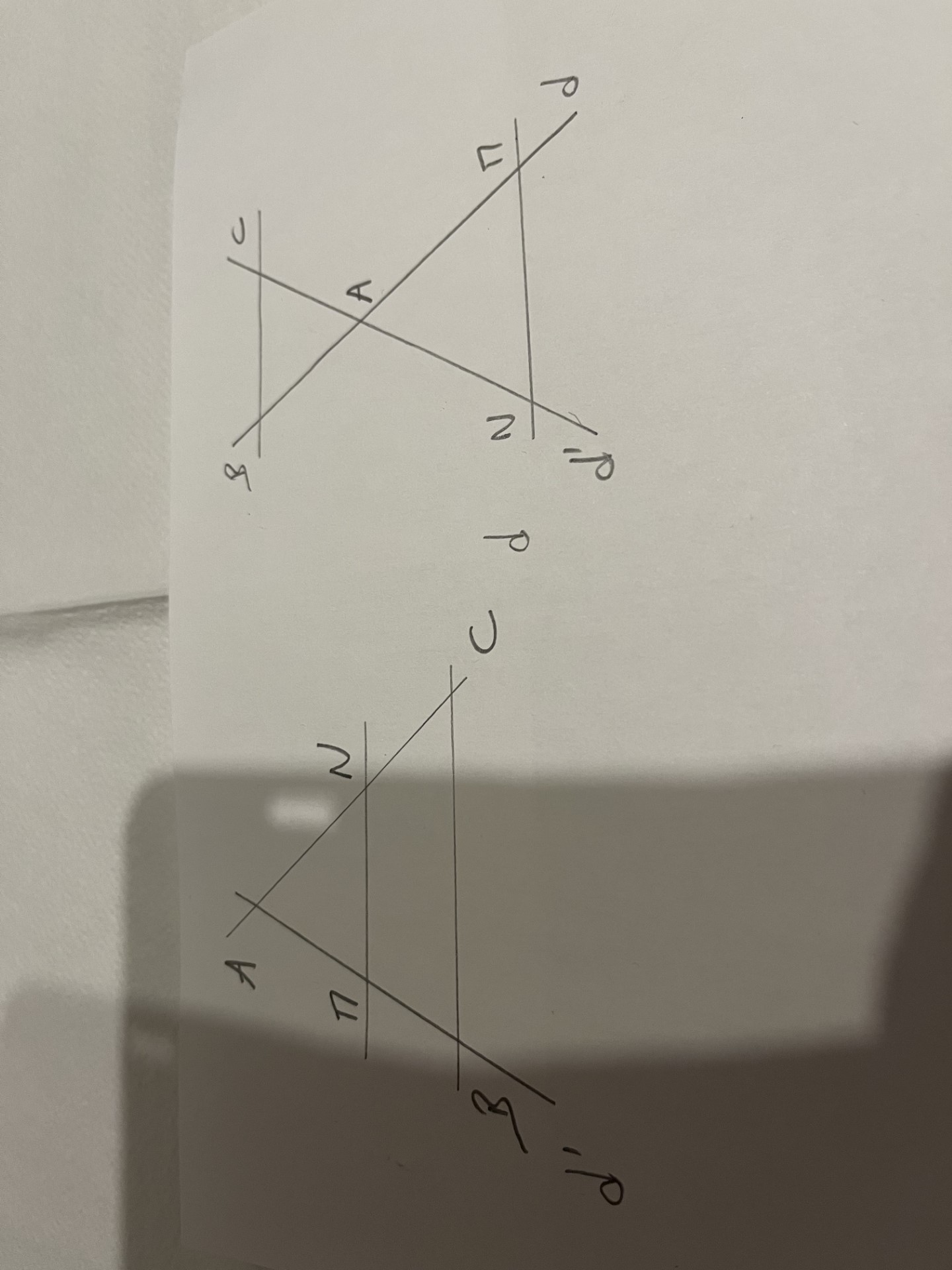



Théorème de Thalès:

Si d et d' sont deux droites sécantes en A.
B et M deux points de d.
C et N deux points de d'.
et (MN) // (BC) alors:
AM/AB = AN/AC = MN/BC

Réciproque du théorème de Thalès:

Si d et d' sont deux droites sécantes en A.
B et M deux points de d.
C et N deux points de d'.
Si A, B et M sont alignés dans le meme ordre que A C et N et que
AM/AB = AN/AC alors:
(MN) // (BC).

Remarque:

Le théorème de Thalès sert a calculer des longeurs.
La réciproque sert a démontrer que deux droites sont parallèles.

2.Agrandissement/Réduction.

a.Définitions

Soit k un nombre positif , l'agrandissement d'une figure par k ou la réduction de la figure
par k est une figure dont les longeurs sont multipliés par k.
si k<1 c'est une réduction alors k est le coefficient de réduction.
si k>1 c'est un agrandissement alors k est le coefficient d'agrandissement.

b.Exemples:

Le triangle (ABC) est un agrandissement du triangle (AMN) de coefficient AB/AM.
et donc (AMN) est une réduction du triangle (ABC) de coefficient AM/AB.

c.Propriétés.

• Dans un agrandissement ou une réduction les angles sont conservés.
• Dans un agrandissement ou une réduction de rapport k les aires sont multipliés par k².
  Les volumes sont multipliés par k³.
  
  

3.Triangles semblables et homothétie.

a.Triangles semblables

Deux triangles sont semblables si les angles de l'un sont égaux aux angles de l'autre. Deux triangles sont semblables si et seulement si les cotés sont proportionels deux a deux cad l'un est l'agrandissement de l'autre ou la reduction de l'autre.

b.Homothétie

1.Définition

On appelle homothétie de centre O et de rapport k la transformation du plan notée h(O;k) qui a tout point M du plan on associe M' tel que :
Si k>0 M' est du meme coté que M par rapport a O et OM' = k OM.M' ∈ [OM)
Si k<0 M' est de l'autre coté de M par rapport a O et OM' = -k OM.

2.Propriétés

L'homothétie de centre O et de rapport -1 est la symétrie centrale.OM' = OM.
Les points O M et M' sont alignés.
Les homothéties conservent le parallélisme les angles mais pas les distances.Les images de figures de
référence restent des figures de références.Un triangle reste un triangle...

3.Liens avec les configurations de Thalès

Les triangles ABC et ADE sont semblables.
Le triangle ADE est une reduction du triangle ABC de rapport k (si k>0)et -k (si k<0).
Le triangle ADE est l'image du triangle (ABC) par homothétie de centre A et de rapport k.